Electronics and Informatics / Measurement of Single-Phase Electric Power
Measurement of Single-Phase Electric Power
1. 목적
단상교류회로에 있어서의 부하 소비전력을 단상 전력계로 측정하고, 전력 및 역률의 개념을 이해한다.
2. 이론
2.1 교류전력
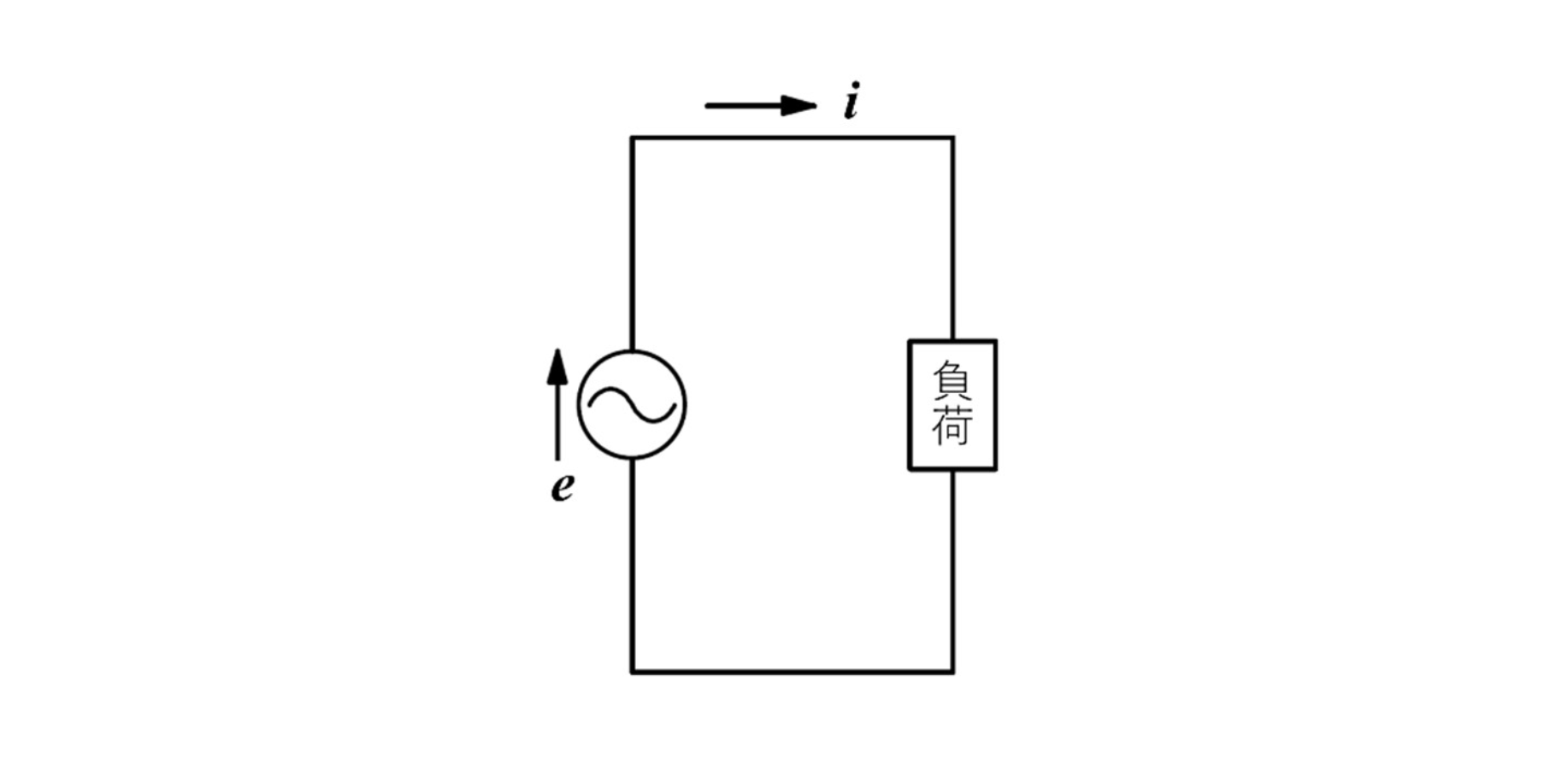
$[Fig.\,1]$ 교류회로
$[Fig.\,1]$의 회로에 가해지는 전압 $e$와 이것에 따라 흐르는 전류 $i$를
\[e=E_{m} \sin (\omega t+\varphi)[\mathrm{V}], \quad i=I_{m} \sin (\omega t+\varphi-\theta)[\mathrm{A}]\]라고 하면, 부하에 공급되는 전력의 순시값 $p$는 다음과 같다.
\[\begin{aligned} p &=e i=E_{m} I_{m} \sin (\omega t+\varphi) \sin (\omega t+\varphi-\theta) \\ &=\frac{1}{2} E_{m} I_{m}\{\cos \theta-\cos (2 \omega t+2 \varphi-\theta)\} \\ &=E I \cos \theta-E I \cos (2 \omega t+2 \varphi-\theta) \end{aligned}\]$[1]$
즉, 순시전력 $p$는 시간에 관계없는 직류성분과 전압, 전류의 2배의 주파수를 갖는 교류성분과의 합으로부터 성립한다. 순시전력은 시시각각 변화하지만, 1주기 동안에 이루어지는 일은 일정하기 때문에 교류전력 $p$는 1주기의 평균전력으로 정의된다. 식$[1]$의 1주기의 평균값을 구하면 제2항은 $0$이 되기 때문에 다음 식으로 나타내어진다.
\[P=\frac{1}{T} \int_{0}^{T} p d t=E I \cos \theta\]$[2]$
여기서 $E$, $I$는 전압과 전류의 실효값이며, $\theta$는 전압과 전류의 위상차를 나타낸다. 교류전력은 전압, 전류의 실효값의 곱에 전압, 전류의 위상차의 여현승을 한 것이다. 이 $cos \theta$를 역률(power factor)이라고 한다.
다음으로 전압, 전류를 벡터표시한 것 같이 전력을 벡터(전력벡터 또는 벡터전력)로 나타내면,
\[\begin{array}{l} \dot{P}=\dot{E} \dot{I}=E \Delta \varphi \cdot I / \varphi-\theta=E I \underline{2 \varphi-\theta} \\ =E I \cos (2 \varphi-\theta)+j E I \sin (2 \varphi-\theta) \end{array}\]가 되며, 그대로 곱을 구한 경우 $2 \Delta$라는 여분이 더해져 식$[2]$를 만족하지 않는다. 따라서 전력을 벡터표시하는 경우, 전압과 전류의 한쪽의 켤레벡터를 이용한다.
\[\begin{aligned} \dot{P} &=\bar{E} \dot{I}=E /-\varphi \cdot I \Delta \varphi-\theta=E I \Delta-\theta \\ =& E I \cos \theta-j E I \sin \theta \end{aligned}\]$[3]$
\[\begin{array}{l} \dot{P}=\dot{E} \bar{I}=E / \varphi \cdot I \underline{-\varphi+\theta}=E I / \theta \\ =E I \cos \theta+j E I \sin \theta \end{array}\]$[4]$
위와 같이 두 식은 벡터의 켤레관계에 있으며, 둘 다 실수부는 교류전력 $P$를 나타내며, 식$[2]$를 만족하고있다. 그리고 전력벡터 $\dot{P}$의 절댓값을 피상전력 $P_a$[VA], 실수부를 유효전력(소비전력 또는 간단하게 전력이라고 한다) $P$[W], 허수부를 무효전력 $Q$[Var]이라고 한다. (Var: Volt ampere reactive)
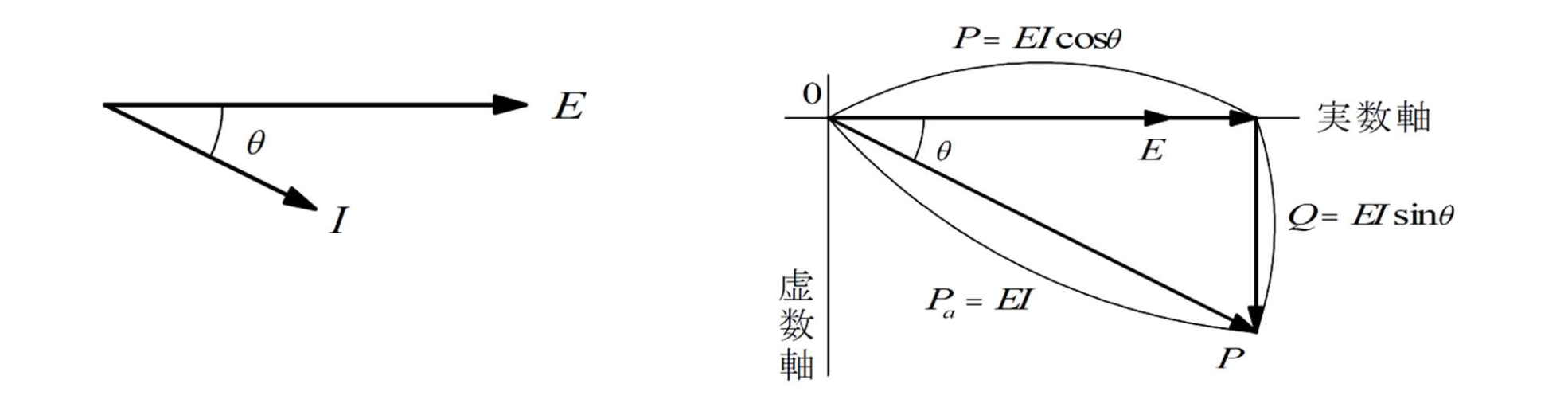
전압을 기준벡터로서 전압, 전류 및 식$[3]$을 벡터도에 나타내면 $[Fig.\,2]$에 나타낸 것 처럼 지연전류에 대해서 지연무효전력이 되며, 전류와 무효전력과의 부합이 일치한다.
$[Fig.\,2]$ 전압, 전류, 전력 벡터도
따라서, 전력의 벡터표시는 일반적으로 전압의 켤레벡터 $\bar{E}$를 사용한다. 고로,
\[\begin{aligned} \dot{P} &=\bar{E} \dot{I}=E I / \underline{\pm} \theta=E I \cos \theta \pm j E I \sin \theta \\ &=P_{a} / \underline\pm \theta=P \pm j Q \end{aligned}\]$[5]$
\[\begin{array}{l} \text { 皮相電力 } P_{a}=E I \quad[\mathrm{VA}]\\ \text { 有交電力 } \quad P=E I \cos \theta \quad[\mathrm{W}]\\ \text { 無交電力 } \quad Q=E I \sin \theta \quad[\mathrm{Var}] \end{array}\]$[6]$
또한, 유효전력은 식$[3]$, $[4]$로부터 다음과 같이 나태낼 수 있다.
\[P=\frac{1}{2}(\bar{E} \dot{I}+\dot{E} \vec{I})\]$[7]$
2.2 단상전력계에 따른 방법
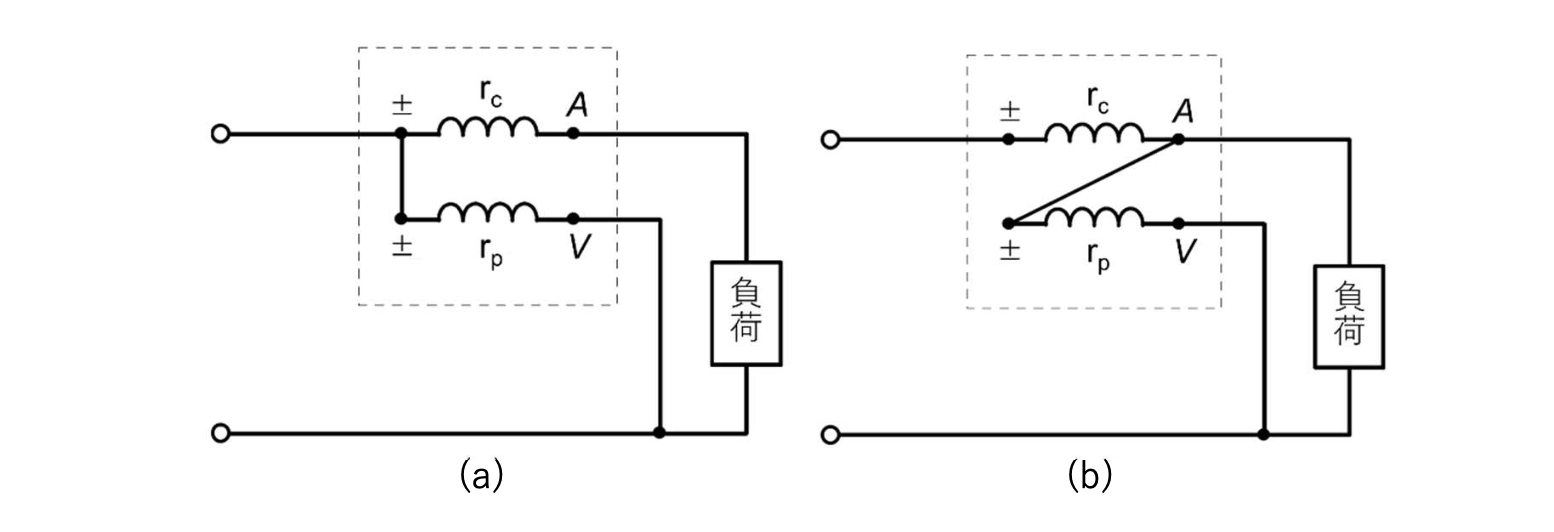
단상전력계는 전류코일과 전압코일을 가지는 전류력계형 계기로, 양 코일의 사이에 작용하는 전자력이 전류와 전압과의 곱에 비례하는 것을 이용해 전력을 측정한다. 전력계를 이용하는 경우, $[Fig.\,3]$에 나타낸 것처럼 코인의 접속법에 따라 오차가 달라진다.
$[Fig.\,3]$ 단상전력계의 구성
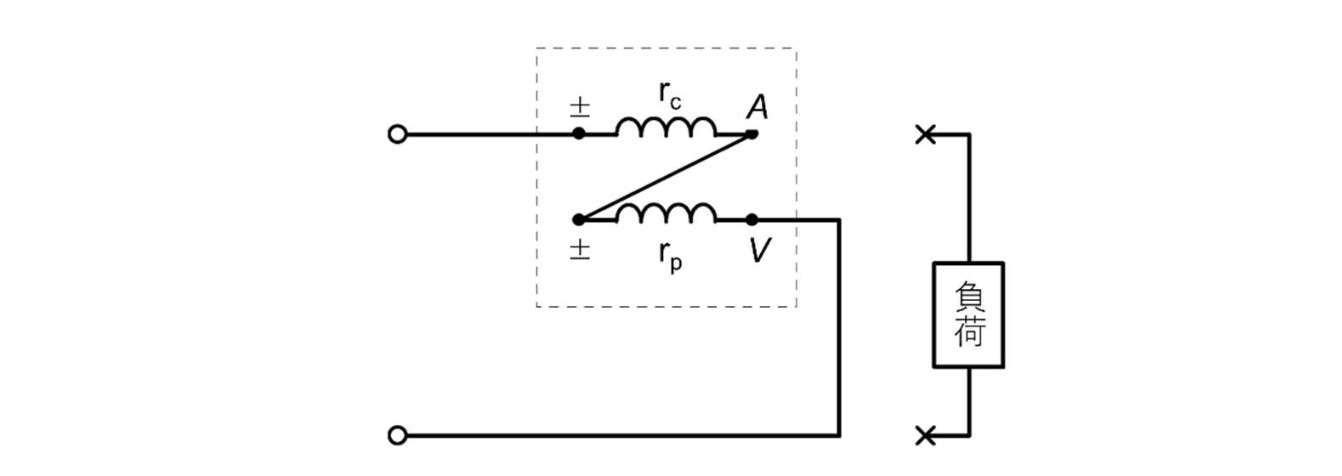
$(a)$의 경우, 전류코일 $r_c$의 손실이 포함되어있으며, $(b)$의 경우에는 전압코일 $r_p$의 손실이 포함되어있다. 따라서 어느쪽의 경우에도 오차가 포함되어있지만, 일반적으로 전류코일의 소비전력이 전압코일의 소비전력보다 꽤 작기 때문에, 교정을 하지 않을 경우 $(a)$의 접속이 이용되며, 교정을 한 경우 $(b)$의 접속이 이용된다. $(b)$의 접속에 있어서 전압코일의 손실은 $[Fig.\,4]$에 나타낸 것과 같이 부하를 분리했을 때의 전력계의 지시에 의해 구해진다.
$[Fig.\,4]$ 전압코일의 손실측정