Neural Network Basic / 7. Multi-Layer Perceptron
7. Multi-Layer Perceptron
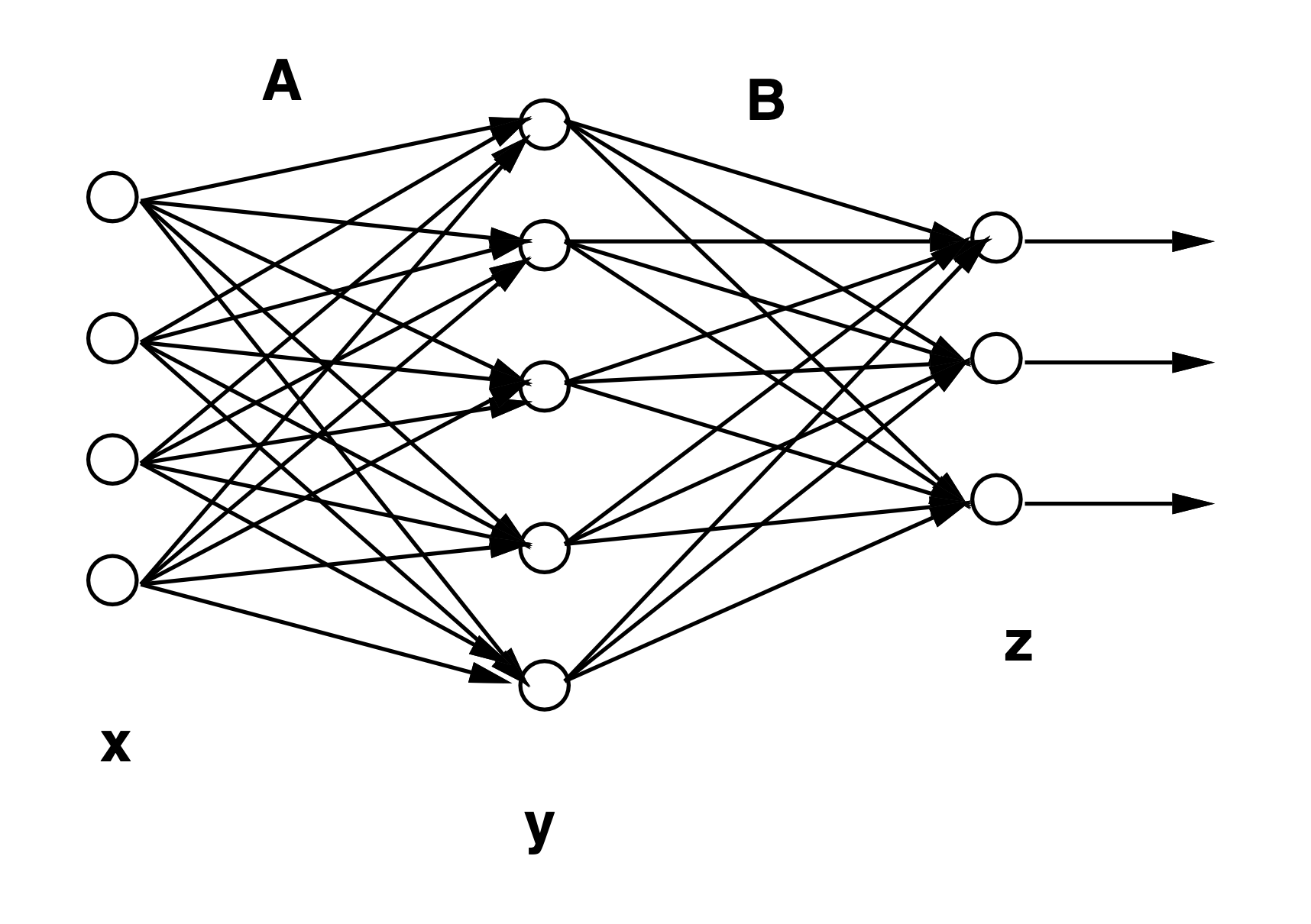
$[Fig.\,5]$ Multi-Layer Perceptron
다층 퍼셉트론은 퍼셉트론을 층상으로 연결한 네트워크이다. 1980년대 오차역전파 알고리즘을 제안하면서 주목받게 되었다. 그 이후 패턴 인식 뿐 만 아니라, 다양한 용도로 활용되어 그 유효성을 확인할 수 있게 되었다.
예를들어, $I$개의 입력신호 조합 $x=(x_1,x_2,…,x_I)^T$에 대해서 $K$개의 출력신호 조합 $z=(z_1,…,z_K)^T)$를 출력하는 중간층이 $1$개의 다층 퍼셉트론은
\[\begin{aligned} \zeta_{j} &=\sum_{i=1}^{1} a_{i j} x_{i}+a_{0 j} \\ y_{j} &=S\left(\zeta_{j}\right) \\ z_{k} &=\sum_{j=1}^{J} b_{j k} y_{j}+b_{0 k} \end{aligned}\]$[45]$
와 같은 식으로 표현할 수 있다. 여기서, $y_j$는 $j$번째의 중간층 뉴런의 출력이다. 또한, $a_{i j}$는 $i$번째의 입력에서 중간층인 $j$번째 뉴런으로의 결합하중이고, $b_{j k}$는 중간층 $j$번째의 뉴런에서 출력층 $k$번째 뉴런으로의 결합하중이다. $[Fig.\,5]$는 그 개념도이다.
이와 같은 다층 퍼셉트론의 능력, 즉 어떤 함수가 표현가능한가에 관해 맥 강력한 결과가 얻어지고 있다. 이것은 중간층이 1층인 다층 퍼셉트론에 의해 임의의 연속함수가 근사 가능하다는 것이다. 물론 임의의 연속함수를 근사하기 위해서는 중가능의 유닛 수를 매우 많게 할 필요가 있을 수 도 있다. 이 결과는 다층 퍼셉트론을 입출력 관계를 학습 시키기 위해서 사용하려면 이론적으로 중간층이 1층인 네트워크로 충분하다는 것을 나타내고 있다.
7.0.1. Backpropagation
다층 퍼셉트론은 임의의 연속함수를 근사하기에 충분한 표현능력을 가지고 있는데 그러한 네트워크에 원하는 정보처리를 시키기 위해서는 뉴런간의 결합하중을 적절한 것으로 설정해야 한다. 뉴런의 수가 증가하면 결합하중의 수도 증가하고, 그것들을 일일이 사람의 힘으로 설정하는 것은 매우 어렵기 때문에 일반적으로는 이용 가능한 데이터로부터 학습에 의해 적절한 결합가중을 준다. 이를 위한 알고리즘으로 가장 유명한 것이 오차 역전파 알고리즘이다. 이 알고리즘은 최단강하법을 이용해서 최적의 파라미터를 구한다.
$N$개의 학습용 데이터를 ${\boldsymbol x_{p}, \boldsymbol t_{p} \mid p=1, \ldots, N}$라고 하자. 학습을 위한 평가기준으로서는 평균제곱오차를 최소로 하는 기준
\[\varepsilon^{2}=\frac{1}{N} \sum_{p=1}^{N}\left\|\boldsymbol{t}_{p}-\boldsymbol{z}_{p}\right\|^{2}=\frac{1}{N} \sum_{p=1}^{N} \varepsilon^{2}(p)\]$[46]$
을 이용하는 것으로 한다. 최급강하법을 적용하기위해서 지금까지와 마찬가지로 평균제곱오차 $\varepsilon^2$의 결합하중에 대한 편미분을 계산하면
\[\begin{aligned} \frac{\partial \varepsilon^{2}}{\partial a_{i j}} &=\frac{1}{N} \sum_{p=1}^{N} \frac{\partial \varepsilon^{2}}{\partial a_{i j}}=\frac{1}{N} \sum_{p=1}^{N}-2 \gamma_{p j} \nu_{p j} x_{p i} \\ \frac{\partial \varepsilon^{2}}{\partial b_{j k}} &=\frac{1}{N} \sum_{p=1}^{N} \frac{\partial \varepsilon^{2}(p)}{\partial b_{j k}}=\frac{1}{N} \sum_{p=1}^{N}-2 \delta_{p k} y_{p j} \end{aligned}\]$[47]$
과 같이 된다. 단,
\[\begin{aligned} \nu_{p j} &=y_{p j}\left(1-y_{p j}\right) \\ \gamma_{p j} &=\sum_{k=1}^{K} \delta_{p k} b_{j k} \\ \delta_{p k} &=t_{p k}-z_{p k} \end{aligned}\]$[48]$
이다. 여기서 $a_{0 j}$ 및 $b_{0 k}$의 계산도 통일적으로 나타내기 위해서 $x_{p 0}=1$ 및 $y_{p 0}=1$이라고 하고있다.따사서, 최급강하법에 의한 결합하중의 갱신식은
\[\begin{aligned} a_{i j} & \Leftarrow a_{i j}-\alpha \frac{\partial \varepsilon^{2}}{\partial a_{i j}} \\ b_{j k} & \Leftarrow b_{j k}-\alpha \frac{\partial \varepsilon^{2}}{\partial b_{j k}} \end{aligned}\]$[49]$
와 같이 된다. 여기서, $\alpha$는 학습률이라고 불리는 양의 파라미터이다.
이 학습 알고리즘은 교사 신호와. 네트워크 출력과의 오차 $\delta$를 결합하중 $b_{j k}$을 통해 역방향으로 $\gamma$를 계산한다고 해석할 수 있기 때문에 오차역전파 알고리즘이라는 이름이 붙여졌다.
이상, Neural Network Basic 끝.