Neural Network Basic / 3. Method of Least Squares
3. Method of Least Squares
최소제곱법 또는 최소근사법이라고 불리는 방법은 어느 변량(설명변수)과 그 변량에 대한 희망 결과(목적 변수, 교사 신호)가 학습 데이터로서 주어졌을 때, 설명 변수에서 목적 변수를 예측하는 모델을 구축하기 위한 통계적 데이터 분석방법으로, 가장 기본적으로, 넓게 이용되고 있다. 아래와 같은 예제에 대한 프로그램을 작성해본다.
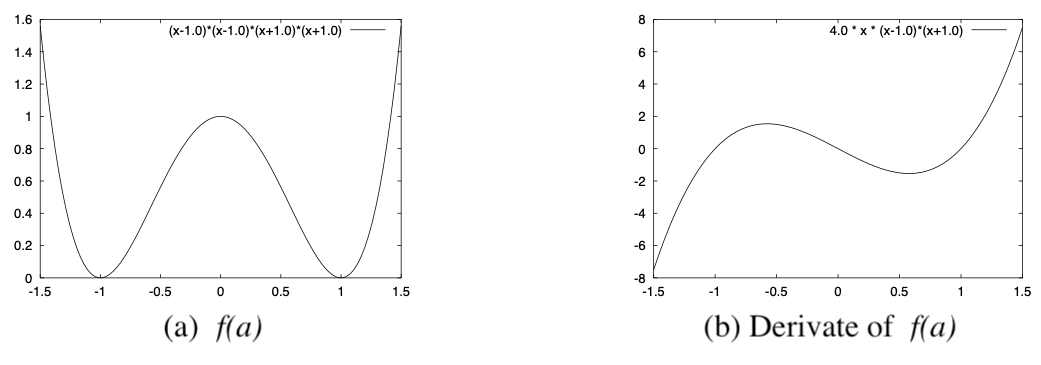
$[Fig.\,2]$ Evaluation Fuction $f(a)$ and its Differentiation
| 학번 | 거리(m) | 악력(kg) | 신장(cm) | 체중(kg) |
|---|---|---|---|---|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 22 36 24 22 27 29 26 23 31 24 23 27 31 25 23 | 28 46 39 25 34 29 38 23 42 27 35 39 38 32 25 | 146 169 160 156 161 168 154 153 160 152 155 154 157 162 142 | 34 57 48 38 47 50 54 40 62 39 46 54 57 53 32 |
$[Table\,1]$ Pitching Record, Grip Strength, Height, and Weight Data
즉, 중학생 투구 기록($t$)과, 악력($x1$), 신장($x2$), 체중($x3$) 데이터를 ${<t_l,x1_l,x2_l,x3_l>\mid l=1,…,15}$라고 하면, $l$번째 학생의 투구 기록을
\[y(x1_l, x2_l, x3_l) = a_0+a_1x1_l+a_2x2_l+a_3x3_l\]$[10]$
으로 예측한다. 이 모델에는 a_0, a_1, a_2, a_3 4개의 파라미터가 포함되어있다. 이 파라미터를 학습용 데이터에서 결정해야 한다. 최소제곱법에서는 예측을 위한 선형 모델 평가기준으로서, 희망 결과와 모델이 예측한 결과의 오차에 제곱한 값의 기대치(평균 제곱 오차)를 사용하여 제곱 오차가 가장 작아지도록 하는 파라미터를 탐색한다. 이 예제에서는 설명변수 조합 $<x1_l,x2_l,x3_l>$에 대한 원하는 결과가 $t_l$이고 모델의 출력이 $y_l$이므로 그 오차 ($t_l-y_l$) 제곱의 평균(평균 제곱 오차) $\varepsilon^2(a0,a1,a2,a3)$는
\[\varepsilon^{2}\left(a_{0}, a_{1}, a_{2}, a_{3}\right)=\frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-y_{l}\right)^{2}=\frac{1}{15} \sum_{l=1}^{15}\left\{t_{l}-\left(a_{0}+a_{1} x 1_{l}+a_{2} x 2_{l}+a_{3} x 3_{l}\right)\right\}^{2}\]$[11]$
과 같이 된다.
이 문제에서는 평가 함수 $\varepsilon^2(a0,a1,a2,a3)$는 각 파라미터에 대해서 2차 함수이기 때문에 아래와 같은 방법으로 최적 파라미터를 구할 수 있다.
최소제곱법의 해석
식[11]의 파라미터 $a_0$에 관한 미분을 구하면
\[\begin{aligned} \frac{\partial \varepsilon^{2}}{\partial a_{0}}=-2\left\{\left(\frac{1}{15} \sum_{l=1}^{15} t_{l}\right)-a_{0}\left(\frac{1}{15} \sum_{l=1}^{15} 1\right)-a_{1}\left(\frac{1}{15} \sum_{l=1}^{15} x 1_{l}\right)-\right.&\left.a_{2}\left(\frac{1}{15} \sum_{l=1}^{15} x 2_{l}\right)-a_{3}\left(\frac{1}{15} \sum_{l=1}^{15} x 3_{l}\right)\right\} \\ &=-2\left\{\bar{t}-a_{0}-a_{1} \bar{x} 1-a_{2} \bar{x} 2-a_{3} \bar{x} 3\right\} \end{aligned}\]$[12]$
와 같이 된다. 최적인 해는 이 값이 $0$이 되는 것이 필요하기에 $\frac{\partial \varepsilon^2}{\partial a_0}=0$으로 두면
\[a_{0}=\bar{t}-a_{1} \bar{x} 1-a_{2} \bar{x} 2-a_{3} \bar{x} 3\]$[13]$
을 얻을 수 있다. 여기서 $\bar t, \bar x1, \bar x2, \bar x3$은 각각 $t, x1, x2, x3$의 평균값으로,
\[\begin{aligned} \bar{t} &=\frac{1}{15} \sum_{l=1}^{15} t_{l} \\ \bar{x} 1 &=\frac{1}{15} \sum_{l=1}^{15} x 1_{l} \\ \bar{x} 2 &=\frac{1}{15} \sum_{l=1}^{15} x 2_{l} \\ \bar{x} 3 &=\frac{1}{15} \sum_{l=1}^{15} x 3_{l} \end{aligned}\]$[14]$
와 같이 정의된다. 이것을 식[12]에 대입하면
\[y\left(x 1_{l}, x 2_{l}, x 3_{l}\right)=\bar{t}+a_{1}\left(x 1_{l}-\bar{x} 1\right)+a_{2}\left(x 2_{l}-\bar{x} 2\right)+a_{3}\left(x 3_{l}-\bar{x} 3\right)\]$[15]$
와 같이 된다. 따라서 평균 제곱 오차 파라미터 $a_1, a_2, a_3$ 함수로서
\[\begin{aligned} \varepsilon^{2}\left(a_{1}, a_{2}, a_{3}\right) &=\frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-y_{l}\right)^{2} \\ &=\frac{1}{15} \sum_{l=1}^{15}\left\{t_{l}-\bar{t}-a_{1}\left(x 1_{l}-\bar{x} 1\right)-a_{2}\left(x 2_{l}-\bar{x} 2\right)-a_{3}\left(x 3_{l}-\bar{x} 3\right)\right\}^{2} \end{aligned}\]$[16]$
과 같이 쓸 수 있다. 이 평균 제곱 오차를 파라미터 $a_1$로 미분하면
\[\begin{aligned} \frac{\partial \varepsilon^{2}}{\partial a_{1}} &=-\frac{1}{15} \sum_{l=1}^{15}\left\{t_{l}-\bar{t}-a_{1}\left(x 1_{l}-\bar{x} 1\right)-a_{2}\left(x 2_{l}-\bar{x} 2\right)-a_{3}\left(x 3_{l}-\bar{x} 3\right)\right\}\left\{x 1_{l}-\bar{x} 1\right\} \\ &=-\left\{\sigma_{t 1}-a_{1} \sigma_{11}-a_{2} \sigma_{21}-a_{3} \sigma_{31}\right\} \end{aligned}\]$[17]$
이 된다. 이와 같이 평균 제곱 오차를 파라미터 $a_2$와 $a_3$로 미분하면
\[\frac{\partial \varepsilon^{2}}{\partial a_{2}}=-\left\{\sigma_{t 2}-a_{1} \sigma_{12}-a_{2} \sigma_{22}-a_{3} \sigma_{32}\right\}\]$[18]$
\[\frac{\partial \varepsilon^{2}}{\partial a_{3}}=-\left\{\sigma_{t 3}-a_{1} \sigma_{13}-a_{2} \sigma_{23}-a_{3} \sigma_{33}\right\}\]$[19]$
가 된다. 여기서,
\[\begin{array}{l} \sigma_{11}=\frac{1}{15} \sum_{l=1}^{15}\left(x 1_{l}-\bar{x} 1\right)\left(x 1_{l}-\bar{x} 1\right), \\ \sigma_{12}=\frac{1}{15} \sum_{l=1}^{15}\left(x 1_{l}-\bar{x} 1\right)\left(x 2_{l}-\bar{x} 2\right), \\ \sigma_{13}=\frac{1}{15} \sum_{l=1}^{15}\left(x 1_{l}-\bar{x} 1\right)\left(x 3_{l}-\bar{x} 3\right), \\ \sigma_{21}=\frac{1}{15} \sum_{l=1}^{15}\left(x 2_{l}-\bar{x} 2\right)\left(x 1_{l}-\bar{x} 1\right), \\ \sigma_{22}=\frac{1}{15} \sum_{l=1}^{15}\left(x 2_{l}-\bar{x} 2\right)\left(x 2_{l}-\bar{x} 2\right), \\ \sigma_{23}=\frac{1}{15} \sum_{l=1}^{15}\left(x 2_{l}-\overline{x 2}\right)\left(x 3_{l}-\bar{x}\right), \\ \sigma_{31}=\frac{1}{15} \sum_{l=1}^{15}\left(x 3_{l}-\overline{x 3}\right)\left(x 1_{l}-x \overline{1}\right), \\ \sigma_{32}=\frac{1}{15} \sum_{l=1}^{15}\left(x 3_{l}-\bar{x} 3\right)\left(x 2_{l}-\bar{x} 2\right), \\ \sigma_{33}=\frac{1}{15} \sum_{l=1}^{15}\left(x 3_{l}-\overline{x 3}\right)\left(x 3_{l}-\bar{x}\right), \\ \sigma_{t 1}=\frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-\bar{t}\right)\left(x 1_{l}-\bar{x}\right), \\ \sigma_{t 2}=\frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-\bar{t}\right)\left(x 2_{l}-\bar{x} 2\right), \\ \sigma_{t 3}=\frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-\bar{t}\right)\left(x 3_{l}-\bar{x} 3\right) \end{array}\]$[20]$
이 된다. 이것들은 분산 혹은 공분산이라고 불린다. 또한 이들의 정의에서
\[\sigma_{12}=\sigma_{21}, \sigma_{13}=\sigma_{31}, \sigma_{23}=\sigma_{32}\]$[21]$
과 같은 함수가 성립되는 것을 알 수 있다.
최적 파라미터에서는 평균 제곱 오차의 파라미터에 대한 미분이 $0$이 될 것이기 때문에, 그것을 $0$으로 두면 결국
\[\begin{array}{l} a_{1} \sigma_{11}+a_{2} \sigma_{12}+a_{3} \sigma_{13}=\sigma_{t 1} \\ a_{1} \sigma_{21}+a_{2} \sigma_{22}+a_{3} \sigma_{23}=\sigma_{t 2} \\ a_{1} \sigma_{31}+a_{2} \sigma_{32}+a_{3} \sigma_{33}=\sigma_{t 3} \end{array}\]$[22]$
와 같은 연립방정식을 얻을 수 있다. 따라서, 이 연립방정식을 풀기 위한 서브루틴이 있으면 최적 파라미터가 구해진다. 이 연립방정식을 행렬과 벡터를 사용해서 표현하면
\[\Sigma a=\sigma\]$[23]$
가 된다. 여기서 행렬 $\Sigma$와 벡터 $a, \sigma$는
\[\Sigma=\left(\begin{array}{lll} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{array}\right), \quad \boldsymbol{a}=\left(\begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array}\right), \quad \boldsymbol{\sigma}=\left(\begin{array}{c} \sigma_{t 1} \\ \sigma_{t 2} \\ \sigma_{t 3} \end{array}\right)\]$[24]$
와 같이 정의된다. 행렬 $\Sigma$는 분산-공분산 행렬이라고 불린다. 만약 이 행렬 $\Sigma$가 정칙이고 역행렬 $\Sigma^{-1}$이 존재한다고 하면, 위 연립방정식의 양변에 왼쪽부터 역행렬 $\Sigma^{-1}$을 곱해서
\[a=\sum^{-1} \sigma\]$[25]$
와 같이 최적 파라미터가 구해진다. 이 문제에서 분산-공분산 행렬 $\Sigma$는 $3\times 3$ 행렬이고, 그 역행렬은 역행렬 공식에서
\[\Sigma^{-1}=\frac{1}{|\Sigma|}\left(\begin{array}{ccc} \sigma_{22} \sigma_{33}-\sigma_{23}^{2} & -\sigma_{12} \sigma_{33}+\sigma_{13} \sigma_{23} & -\left(-\sigma_{12} \sigma_{23}+\sigma_{13} \sigma_{22}\right) \\ -\sigma_{12} \sigma_{33}+\sigma_{13} \sigma_{23} & \sigma_{11} \sigma_{33}-\sigma_{13}^{2} & -\left(\sigma_{11} \sigma_{23}-\sigma_{12} \sigma_{13}\right) \\ -\left(-\sigma_{12} \sigma_{23}+\sigma_{13} \sigma_{22}\right) & -\left(\sigma_{11} \sigma_{23}-\sigma_{12} \sigma_{13}\right) & \sigma_{11} \sigma_{22}-\sigma_{12}^{2} \end{array}\right)\]$[26]$
과 같이 구해진다. 여기서 $|\Sigma|$는 행렬 $\Sigma$의 행렬식에서 $|\Sigma|=\sigma_{11}\sigma_{22}\sigma_{33}-\sigma_{11}\sigma_{23}^2-\sigma_{12}^2\sigma_{33}-\sigma_{13}^2\sigma_{22}+2\sigma_{12}\sigma_{13}\sigma_{23}$이다. 이 행렬식 $|\Sigma|$가 $0$이 아닌 경우에 역행렬이 존재한다. 즉, 이것이 최적 파라미터를 계산할 수 있는 조건이 된다.
이 식에 따라 투구 기록을 예측하기 위한 최적 파라미터를 구체적으로 계산하면
\[\begin{array}{l} a_{0}=-13.21730 \\ a_{1}=0.20138 \\ a_{2}=0.17103 \\ a_{3}=0.12494 \end{array}\]$[27]$
과 같이 된다. 위와 같이 해서 학습 데이터에서 최적 파라미터가 구해지면, 악력($x1=30$), 신장($x2=165$), 체중($x3=55$)의 데이터에서 투구 기록을
\[y=-13.21730+0.20138 x 30+0.17103 x 165+0.12494 x 55=27.91575\]$[28]$
과 같이 예측할 수 있게 된다. 이 문제의 경우는 행렬$\Sigma$가 $3\times 3$이었기 때문에, 손으로 계산해도 최적해를 구할 수 있지만, 일반적으로는 연립 방정식을 푸는 서브루틴 등을 사용해서 최적해를 구할 필요가 있다.
최급강하법에 따른 파라미터 추정
다음으로 최소제곱법의 최적 파라미터를 선형 방정식을 풀지 않고 최급강하법으로 구하는 프로그램에 대해 생각해보자. 최급강하법은 적당한 초기 파라미터에서 시작해서 파라미터 값을 미분 값과 역방향으로 조금 변화시켜 조금씩 최적 파라미터로 근접해가는 방법이기 때문에 우선, 평가 함수(최소 제곱 법에서는 최소 제곱 오차)의 각 파라미터에서의 미분을 계산할 필요가 있다.
식[11]의 최소제곱오차 파라미터 $a_0$에 대한 미분은
\[\frac{\partial \varepsilon^{2}}{\partial a_{0}}=-2 \frac{1}{15} \sum_{l=1}^{15}\left\{\varepsilon_{l} \frac{\partial \varepsilon_{l}}{\partial a_{0}}\right\}=-2 \frac{1}{15} \sum_{l=1}^{15} \varepsilon_{l}=-2 \frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-y\left(x 1_{l}, x 2_{l}, x 3_{l}\right)\right)\]$[29]$
과 같이 쓸 수 있다.
이와 같이, 최소 제곱 오차 파라미터 $a_1,a_2,a_3$에 대한 미분은
\[\begin{array}{l} \frac{\partial \varepsilon^{2}}{\partial a_{1}}=-2 \frac{1}{15} \sum_{l=1}^{15}\left\{\varepsilon_{l} \frac{\partial \varepsilon_{l}}{\partial a_{1}}\right\}=-2 \frac{1}{15} \sum_{l=1}^{15} \varepsilon_{l} x 1_{l}=-2 \frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-y\left(x 1_{l}, x 2_{l}, x 3_{l}\right)\right) x 1_{l} \\ \frac{\partial \varepsilon^{2}}{\partial a_{2}}=-2 \frac{1}{15} \sum_{l=1}^{15}\left\{\varepsilon_{l} \frac{\partial \varepsilon_{l}}{\partial a_{2}}\right\}=-2 \frac{1}{15} \sum_{l=1}^{15} \varepsilon_{l} x 2_{l}=-2 \frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-y\left(x 1_{l}, x 2_{l}, x 3_{l}\right)\right) x 2_{l} \\ \frac{\partial \varepsilon^{2}}{\partial a_{3}}=-2 \frac{1}{15} \sum_{l=1}^{15}\left\{\varepsilon_{l} \frac{\partial \varepsilon_{l}}{\partial a_{3}}\right\}=-2 \frac{1}{15} \sum_{l=1}^{15} \varepsilon_{l} x 3_{l}=-2 \frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-y\left(x 1_{l}, x 2_{l}, x 3_{l}\right)\right) x 3_{l} \end{array}\]$[30]$
이 된다.
따라서, 최급강하법에 따는 각 파라미터의 갱신식은
\[\begin{array}{l} a_{0}^{(k+1)}=a_{0}^{(k)}-\left.\alpha \frac{\partial \varepsilon^{2}}{\partial a_{0}}\right|_{a_{0}=a_{0}^{(k)}}=a_{0}^{(k)}+2 \alpha \frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-y\left(x 1_{l}, x 2_{l}, x 3_{l}\right)\right) \\ a_{1}^{(k+1)}=a_{1}^{(k)}-\left.\alpha \frac{\partial \varepsilon^{2}}{\partial a_{1}}\right|_{a_{1}=a_{1}^{(k)}}=a_{1}^{(k)}+2 \alpha \frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-y\left(x 1_{l}, x 2_{l}, x 3_{l}\right)\right) x 1_{l} \\ a_{2}^{(k+1)}=a_{2}^{(k)}-\left.\alpha \frac{\partial \varepsilon^{2}}{\partial a_{2}}\right|_{a_{2}=a_{2}^{(k)}}=a_{2}^{(k)}+2 \alpha \frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-y\left(x 1_{l}, x 2_{l}, x 3_{l}\right)\right) x 2_{l} \\ a_{3}^{(k+1)}=a_{3}^{(k)}-\left.\alpha \frac{\partial \varepsilon^{2}}{\partial a_{3}}\right|_{a_{3}=a_{3}^{(k)}}=a_{3}^{(k)}+2 \alpha \frac{1}{15} \sum_{l=1}^{15}\left(t_{l}-y\left(x 1_{l}, x 2_{l}, x 3_{l}\right)\right) x 3_{l} \end{array}\]$[31]$
이 된다.
그럼 이 식을 이용해서 악력($x1$), 신장($x2$), 체중($x3$) 데이터에서 공 던지기 기록($t$)를 예측하기 위한 선형 모델 파라미터를 최급강하법으로 구하는 프로그램을 작성해 보자. 단, 학습을 안정화시키기 위해서 각 변수($x1,x2,x3$)의 값을 10으로 나눠서
\[x 1^{\prime}=\frac{x 1}{100}, x 2^{\prime}=\frac{x 2}{100}, x 3^{\prime}=\frac{x 3}{100}\]$[32]$
와 같이 정규화하고 나서 이용한다. 여기서 학습 계수를 파라미터마다 바꿀 필요가 없어진다.
아래는 그 프로그램의 예시이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
#include <stdio.h>
#define NSAMPLE 15
#define XDIM 3
main() {
FILE * fp;
double t[NSAMPLE];
double x[NSAMPLE][XDIM];
double a[XDIM + 1];
int i, j, l;
double y, err, mse;
double derivatives[XDIM + 1];
double alpha = 0.2; /* Learning Rate */
/* Open Data File */
if ((fp = fopen("ball.dat", "r")) == NULL) {
fprintf(stderr, "File Open Fail\n");
exit(1);
}
/* Read Data */
for (l = 0; l < NSAMPLE; l++) {
/* Teacher Signal (Ball) */
fscanf(fp, "%lf", & (t[l])); /* Input input vectors */
for (j = 0; j < XDIM; j++) {
fscanf(fp, "%lf", & (x[l][j]));
}
}
/* Close Data File */
fclose(fp);
/* Print the data */
for (l = 0; l < NSAMPLE; l++) {
printf("%3d : %8.2f ", l, t[l]);
for (j = 0; j < XDIM; j++) {
printf("%8.2f ", x[l][j]);
}
printf("\n");
}
/* scaling the data */
for (l = 0; l < NSAMPLE; l++) {
/* t[l] = t[l] / tmean;*/
for (j = 0; j < XDIM; j++) {
x[l][j] = x[l][j] / 100.0;
}
}
/* Initialize the parameters by random number */
for (j = 0; j < XDIM + 1; j++) {
a[j] = (drand48() - 0.5);
}
/* Open output file */
fp = fopen("mse.out", "w");
/* Learning the parameters */
for (i = 1; i < 20000; i++) {
/* Learning Loop */
/* Compute derivatives */
/* Initialize derivatives */
for (j = 0; j < XDIM + 1; j++) {
derivatives[j] = 0.0;
}
/* update derivatives */
for (l = 0; l < NSAMPLE; l++) {
/* prediction */
y = a[0];
for (j = 1; j < XDIM + 1; j++) {
y += a[j] * x[l][j - 1];
}
/* error */
err = t[l] - y;
/* printf("err[%d] = %f\n", l, err);*/
/* update derivatives */
derivatives[0] += err;
for (j = 1; j < XDIM + 1; j++) {
derivatives[j] += err * x[l][j - 1];
}
}
for (j = 0; j < XDIM + 1; j++) {
derivatives[j] = -2.0 * derivatives[j] / (double) NSAMPLE;
}
/* update parameters */
for (j = 0; j < XDIM + 1; j++) {
a[j] = a[j] - alpha * derivatives[j];
}
/* Compute Mean Squared Error */
mse = 0.0;
for (l = 0; l < NSAMPLE; l++) {
/* prediction */
y = a[0];
for (j = 1; j < XDIM + 1; j++) {
y += a[j] * x[l][j - 1];
}
/* error */
err = t[l] - y;
mse += err * err;
}
mse = mse / (double) NSAMPLE;
printf("%d : Mean Squared Error is %f\n", i, mse);
fprintf(fp, "%f\n", mse);
}
fclose(fp);
/* Print Estmated Parameters */
for (j = 0; j < XDIM + 1; j++) {
printf("a[%d]=%f, ", j, a[j]);
}
printf("\n");
/* Prediction and Errors */
for (l = 0; l < NSAMPLE; l++) {
/* prediction */
y = a[0];
for (j = 1; j < XDIM + 1; j++) {
y += a[j] * x[l][j - 1];
}
/* error */
err = t[l] - y;
printf("%3d : t = %f, y = %f (err = %f)\n", l, t[l], y, err);
}
}
이 프로그램을 실행시키면
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
a[0]=-13.156891, a[1]=20.077345, a[2]=17.056200, a[3]=12.562173,
0 : t = 22.000000, y = 21.637957 (err = 0.362043)
1 : t = 36.000000, y = 32.064105 (err = 3.935895)
2 : t = 24.000000, y = 27.993037 (err = -3.993037)
3 : t = 22.000000, y = 23.243744 (err = -1.243744)
4 : t = 27.000000, y = 27.034110 (err = -0.034110)
5 : t = 29.000000, y = 27.601042 (err = 1.398958)
6 : t = 26.000000, y = 27.522622 (err = -1.522622)
7 : t = 23.000000, y = 22.581754 (err = 0.418246)
8 : t = 31.000000, y = 30.354062 (err = 0.645938)
9 : t = 24.000000, y = 23.088664 (err = 0.911336)
10 : t = 23.000000, y = 26.085890 (err = -3.085890)
11 : t = 27.000000, y = 27.723396 (err = -0.723396)
12 : t = 31.000000, y = 28.411174 (err = 2.588826)
13 : t = 25.000000, y = 27.556856 (err = -2.556856)
14 : t = 23.000000, y = 20.102145 (err = 2.897855)
와 같은 파라미터가 구해지고, 학습에 이용한 데이터에 대해서 구해진 파라미터를 이용한 모델로 예측한 결과가 표시된다. 파라미터가 먼저 손으로 계산해서 구한 최적 파라미터와 가까운 값으로 수렴하여 공 던지기 기록이 대체로 예측할 수 있게 된 것을 알 수 있다.