Neural Network Basic / 2. Method of Steepest Descent

수업 내용 보호를 위해 일부 생략된 내용이 있을 수 있습니다.

2. Method of Steepest Descent

최급강하법, 안장점 어림, 라플라스 방법, 경사 하강법 모두 같은 의미이다.

주로 학습 문제는 주어진 평가 함수를 최적으로 하는 파라미터를 구하는 문제로 정식화된다. 따라서 이 학습을 위해서는 그 최적화 문제를 풀기 위해서 방법이 필요하다. 최적화 방법에는 간단한 것부터 고속성과 안정성을 위해 고안한 복잡 기법까지, 많은 방법이 있는데 여기에서는 가장 간단한 최적화 방법 중 하나인 최급강하법이라고 불리는 최적화 방법의 기본적인 생각에 대해 이해하고 그 프로그램을 만들어 본다.

예제 1. 어느 파라미터 $a$의 평가척도가 다음과 같은 2차 함수 $$ f(a)=(a-1.0)^{2} $$ $[1]$ 로 주어졌다고 하자. 이때, 이 평가 함수가 가장 최소가 되는 파라미터 $a$의 (최적해)를 구해라.

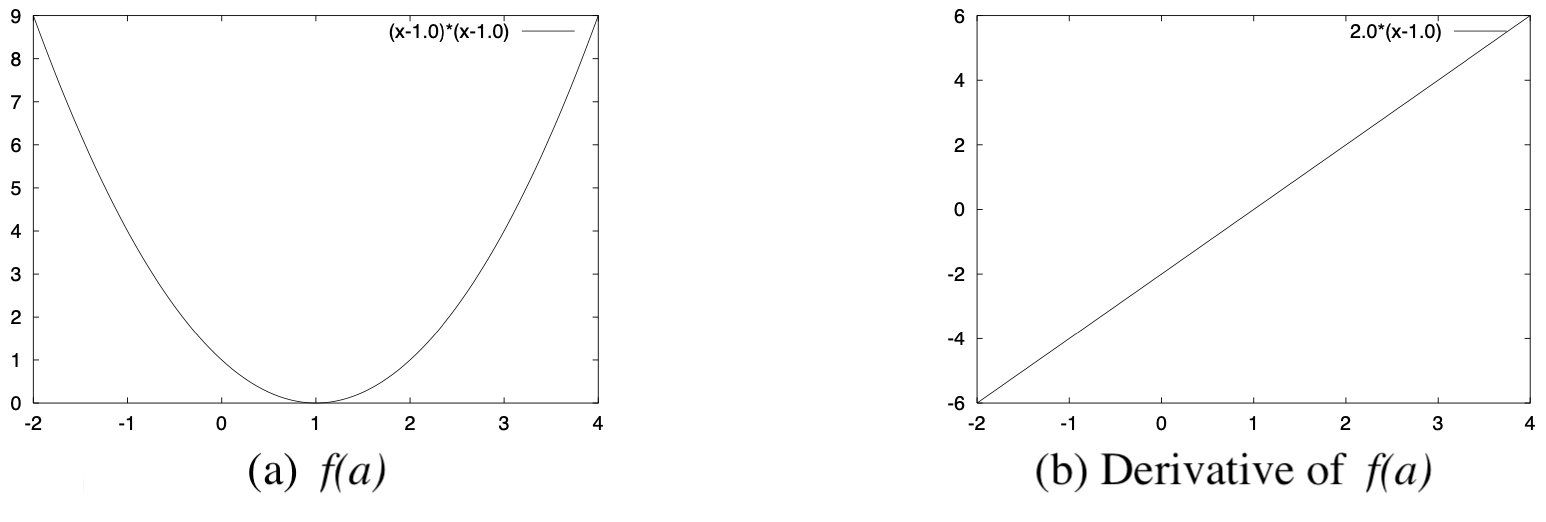
이러한 문제는 일반적으로 최적화 문제라고 불린다. $[Fig.\,1]$ (a)는 평가 함수의 그래프를 나타낸다. 이 문제와 같이 평가 함수 $f(a)$가 파라미터 $a$에 대해서 2차 함수인 경우에는 최적 파라미터는 단 하나로 결정되고, 그 해도 아래와 같은 방법으로 간단하게 구한다.

해석적 해법

식[1]의 파라미터 $a$에 대한 미분을 구하면

\[\frac{\partial f(a)}{\partial a}=2(a-1.0)\]

$[2]$

가 된다. 여기서 2차 평가 함수의 경우, 미분이 $0$이 되는 점이 최소치가 되기 때문에 이 평가 함수를 최소로 하는 최적 $a$는

\[\frac{\partial f(a)}{\partial a}=2(a-1.0)=0\]

$[3]$

$[Fig.\,1]$ Evaluation Fuction $f(a)$ and its Differentiation

에서 $a = 1.0$이라는 것을 알 수 있다. 실제로 식$[1]$의 $a$에 $1.0$을 대입해보면 $f(1.0)=(1.0-1.0)^2=0.0$이 된다. 평가 함수 $f(a)$는 0 이상 함수인 것으로 $a=1.0$에서 최솟값 $0.0$을 얻을 수 있는 것을 확인할 수 있다.

최급강하법

최급강하법은 어느 적당한 초기값(초기 파라미터)에서 시작해서 그 값을 반복 갱신(수정)하는 것으로, 최적 파라미터 값을 구하는 방법(반복 최적화 방법)인 기본적인 간단한 방법이다.

[예제 1]과 같은 평가 함수가 최소가 되는 파라미터를 구하는 문제에서 최급강하법에서의 파라미터 갱신은

\[a^{(k+1)}=a^{(k)}-\left.\alpha \frac{\partial f(a)}{\partial a}\right|_{a=a^{(k)}}\]

$[4]$

와 같이 된다. 여기에서 $a^{(k)}$는 $k$회째 반복해서 얻어진 파라미터 $a$의 추정치로, $\alpha \frac{\partial f(a)}{\partial a} | _{a=a^k}$는 $a=a^{(k)}$에서의 평가 함수 파라미터 $a$에 관한 미분 값이다. 또한, $\alpha$는 1회 반복으로 얼마나 파라미터를 갱신하는가를 제어하는 작은 양의 정수로, 학습관계라고 불리기도 한다. 즉, 최급강하법에서는 파라미터 값을 미분 값과 역방향으로 조금만 변화시켜서 서서히 최적 파라미터로 접근해간다. 때문에 학습 계수 $a$의 값을 크게 하면 1회 반복으로 파라미터 값을 크게 바꿀 수 있지만 너무 크면 최적 파라미터 근처에서 값이 진동하거나 발산해버린다. 반대로, 너무 작게 하면 1회 갱신에서는 파라미터 값이 거의 수정되지 않아서 최적 파라미터가 구해질 때까지 많은 반복이 필요하다. 그래서 최급강하법에서는 이 값을 적절히 설정하는 것이 중요하다.

그럼 [예제 1]의 최적 파라미터 $a$의 값을 최급강하법으로 구하기 위한 구체적인 갱신식을 구해보자.

평가 함수 $f(a)$의 파라미터 $a$에 대한 미분은 먼저 구한

\[\frac{\partial f(a)}{\partial a}=2(a-1.0)\]

$[5]$

와 같이 된다. 이것을 최급강하 갱신식에 대입하면 파라미터 갱신식은

\[a^{(k+1)}=a^{(k)}-2 \alpha\left(a^{(k)}-1.0\right)\]

$[6]$

이 된다. [$Fig.\,1$] (b)에 평가 함수 $f(a)$의 파라미터 $a$에 대한 미분 $\frac{\partial f(a)}{\partial (a)}$의 그래프를 나타낸다. 이 그래프에서 파라미터의 현재 추정치가 $1.0$ 이상인 경우에는 미분은 양수가 되고 현재 $a$의 추정치보다 작은 값으로 갱신되며, 반대로 $1.0$ 이하인 경우에는 미분이 음수가 되고 현재 추정치보다 큰 값으로 갱신된다. 그 결과, 어느 경우라도 $1.0$에 근접하는 방향으로 갱신되게 된다.

이 갱신식을 사용해서 평가 함수가 최소가 되는 $a$의 값(최적해)을 구하는 프로그램을 작성하면 아래와 같다.

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

double f(double a) {
    return ((a - 1.0) * (a - 1.0));
}

double df(double a) {
    return (2.0 * (a - 1.0));
}

int main() {
    double a;
    int i;
    double alpha = 0.1;

    a = 100.0 * (drand48() - 0.5);
    printf("a at 0/99 = %f, ", a);
    printf("of f(a) = %f\n", f(a));

    for (i = 1; i < 100; i++) {
        a = a - alpha * df(a);
        printf("a at %d/99 = %f, ", i, a);
        printf("f(a) = %f\n", f(a));
    }
}

여기에서 함수 $f$는 최적화 하고 싶은 평가 함수(2차 함수)로, 그 미분이 $df$이다. 구하고 싶은 $a$의 최적 값을 랜덤 값으로 초기화하고, 앞의 갱신식에 따라서 100회 갱신한다. 갱신할 때의 학습 계수는 $alpha$로, 이 프로그램에서는 $0.1$로 설정했다.

이 프로그램을 컴파일해서 실행시키면 아래와 같은 결과를 얻을 수 있다.

a at 0/99 = -50.000000, of f(a) = 2601.000000
a at 1/99 = -39.800000, f(a) = 1664.640000
a at 2/99 = -31.640000, f(a) = 1065.369600
a at 3/99 = -25.112000, f(a) = 681.836544
a at 4/99 = -19.889600, f(a) = 436.375388
a at 5/99 = -15.711680, f(a) = 279.280248
a at 6/99 = -12.369344, f(a) = 178.739359
a at 7/99 = -9.695475, f(a) = 114.393190
a at 8/99 = -7.556380, f(a) = 73.211641
a at 9/99 = -5.845104, f(a) = 46.855451
a at 10/99 = -4.476083, f(a) = 29.987488
a at 11/99 = -3.380867, f(a) = 19.191993
a at 12/99 = -2.504693, f(a) = 12.282875
a at 13/99 = -1.803755, f(a) = 7.861040
a at 14/99 = -1.243004, f(a) = 5.031066
a at 15/99 = -0.794403, f(a) = 3.219882
a at 16/99 = -0.435522, f(a) = 2.060725
a at 17/99 = -0.148418, f(a) = 1.318864
a at 18/99 = 0.081266, f(a) = 0.844073
a at 19/99 = 0.265013, f(a) = 0.540207
a at 20/99 = 0.412010, f(a) = 0.345732
a at 21/99 = 0.529608, f(a) = 0.221269
a at 22/99 = 0.623686, f(a) = 0.141612
a at 23/99 = 0.698949, f(a) = 0.090632
a at 24/99 = 0.759159, f(a) = 0.058004
a at 25/99 = 0.807327, f(a) = 0.037123
a at 26/99 = 0.845862, f(a) = 0.023759
a at 27/99 = 0.876690, f(a) = 0.015205
a at 28/99 = 0.901352, f(a) = 0.009731
a at 29/99 = 0.921081, f(a) = 0.006228
a at 30/99 = 0.936865, f(a) = 0.003986
a at 31/99 = 0.949492, f(a) = 0.002551
a at 32/99 = 0.959594, f(a) = 0.001633
a at 33/99 = 0.967675, f(a) = 0.001045
a at 34/99 = 0.974140, f(a) = 0.000669
a at 35/99 = 0.979312, f(a) = 0.000428
a at 36/99 = 0.983450, f(a) = 0.000274
a at 37/99 = 0.986760, f(a) = 0.000175
a at 38/99 = 0.989408, f(a) = 0.000112
a at 39/99 = 0.991526, f(a) = 0.000072
a at 40/99 = 0.993221, f(a) = 0.000046
a at 41/99 = 0.994577, f(a) = 0.000029
a at 42/99 = 0.995661, f(a) = 0.000019
a at 43/99 = 0.996529, f(a) = 0.000012
a at 44/99 = 0.997223, f(a) = 0.000008
a at 45/99 = 0.997779, f(a) = 0.000005
a at 46/99 = 0.998223, f(a) = 0.000003
a at 47/99 = 0.998578, f(a) = 0.000002
a at 48/99 = 0.998863, f(a) = 0.000001
a at 49/99 = 0.999090, f(a) = 0.000001
a at 50/99 = 0.999272, f(a) = 0.000001
a at 51/99 = 0.999418, f(a) = 0.000000
a at 52/99 = 0.999534, f(a) = 0.000000
a at 53/99 = 0.999627, f(a) = 0.000000
a at 54/99 = 0.999702, f(a) = 0.000000
a at 55/99 = 0.999761, f(a) = 0.000000
a at 56/99 = 0.999809, f(a) = 0.000000
a at 57/99 = 0.999847, f(a) = 0.000000
a at 58/99 = 0.999878, f(a) = 0.000000
a at 59/99 = 0.999902, f(a) = 0.000000
a at 60/99 = 0.999922, f(a) = 0.000000
a at 61/99 = 0.999937, f(a) = 0.000000
a at 62/99 = 0.999950, f(a) = 0.000000
a at 63/99 = 0.999960, f(a) = 0.000000
a at 64/99 = 0.999968, f(a) = 0.000000
a at 65/99 = 0.999974, f(a) = 0.000000
a at 66/99 = 0.999980, f(a) = 0.000000
a at 67/99 = 0.999984, f(a) = 0.000000
a at 68/99 = 0.999987, f(a) = 0.000000
a at 69/99 = 0.999990, f(a) = 0.000000
a at 70/99 = 0.999992, f(a) = 0.000000
a at 71/99 = 0.999993, f(a) = 0.000000
a at 72/99 = 0.999995, f(a) = 0.000000
a at 73/99 = 0.999996, f(a) = 0.000000
a at 74/99 = 0.999997, f(a) = 0.000000
a at 75/99 = 0.999997, f(a) = 0.000000
a at 76/99 = 0.999998, f(a) = 0.000000
a at 77/99 = 0.999998, f(a) = 0.000000
a at 78/99 = 0.999999, f(a) = 0.000000
a at 79/99 = 0.999999, f(a) = 0.000000
a at 80/99 = 0.999999, f(a) = 0.000000
a at 81/99 = 0.999999, f(a) = 0.000000
a at 82/99 = 0.999999, f(a) = 0.000000
a at 83/99 = 1.000000, f(a) = 0.000000
a at 84/99 = 1.000000, f(a) = 0.000000
a at 85/99 = 1.000000, f(a) = 0.000000
a at 86/99 = 1.000000, f(a) = 0.000000
a at 87/99 = 1.000000, f(a) = 0.000000
a at 88/99 = 1.000000, f(a) = 0.000000
a at 89/99 = 1.000000, f(a) = 0.000000
a at 90/99 = 1.000000, f(a) = 0.000000
a at 91/99 = 1.000000, f(a) = 0.000000
a at 92/99 = 1.000000, f(a) = 0.000000
a at 93/99 = 1.000000, f(a) = 0.000000
a at 94/99 = 1.000000, f(a) = 0.000000
a at 95/99 = 1.000000, f(a) = 0.000000
a at 96/99 = 1.000000, f(a) = 0.000000
a at 97/99 = 1.000000, f(a) = 0.000000
a at 98/99 = 1.000000, f(a) = 0.000000
a at 99/99 = 1.000000, f(a) = 0.000000

파라미터 $a$의 갱신이 반복되면 점차 $1.0$에 가까워지고 동시에 평가 함수 $f(a)$의 값이 $0.0$에 가까워지는 모습을 알 수 있다.