Control Engineering / 1. Linear Differential Equation and Transfer Function
1. Linear Differential Equation and Transfer Function
1.1. Differential Equation and Transfer Function
수학 모델의 미분 방정식을 구한다고 해 보자. 이 때, 입력input과 출력output의 선택에 주의한다. 입력이란 힘이나 전압 등 자유롭게 조작할 수 있는 변수variable이다. 출력이란 제어할 양(제어량controlled variable)으로서 주목하는 변수이다.
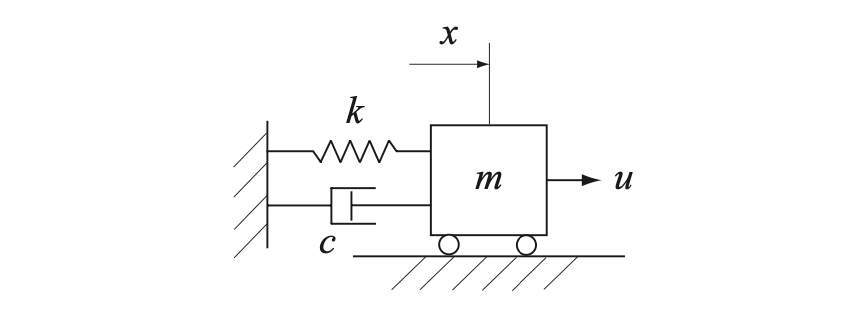
$[Fig.\,1.1]$ Damped One-Degree System
$[Fig.\,1.1]$의 1자유도 감쇠계damped one-degree system의 수학정 모델을 구해보자. $x$는 물체의 변위displacement, $u$는 물체에 작용하는 힘force, $m$은 질량mass, $k$는 용수철 상수spring constant, $c$는 점성감쇠계수viscous damping coefficient이다. 달랑베르의 원리D’Alembert’s principle (동적인 힘을 포함하여 힘의 균형식을 세울 수 있다는 원리)에 따라 운동방정식equation of motion을 포함하면
즉
\[m \ddot{x}+c \dot{x}+k x=u\]$[1.1]$
을 얻을 수 있다. 이 경우, 입력은 $u$이다. 출력($y$로 나타낸다)으로서는, $x$나 $\ddot{x}$, 또는 이들의 선형결합
\[y=b_{0} x+b_{1} \dot{x}\]$[1.2]$
등을 생각할 수 있다. $y$가 $[1.2]$식에서 주어진 경우, $y$와 $u$에 관한 미분방정식을 구해보자. $[1.1]$식에 $b_0$을 곱한다.
\[b_{0}(m \ddot{x}+c \dot{x}+k x)=b_{0} u\]$[1.1]$식을 $t$로 미분하고, $b_1$를 곱한다.
\[b_{1}\left(m x^{(3)}+c \ddot{x}+k \dot{x}\right)=b_{1} \dot{u}\]이것을 각 변끼리 더하면
\[m\left(b_{0} \ddot{x}+b_{1} x^{(3)}\right)+c\left(b_{0} \dot{x}+b_{1} \ddot{x}\right)+k\left(b_{0} x+b_{1} \dot{x}\right)=b_{0} u+b_{1} \dot{u}\]즉
\[m \ddot{y}+c \dot{y}+k y=b_{0} u+b_{1} \dot{u}\]$[1.3]$
을 얻는다.
광범위한 수학 모델을 $[1.3]$식과 같은 미분방정식으로 표현할 수 있다. 제어공학에서 다루는 미분방정식의 일반형은 다음과 같다.
$$ \frac{d^{n} y}{d t^{n}}+a_{n-1} \frac{d^{n-1} y}{d t^{n-1}}+\cdots+a_{1} \frac{d y}{d t}+a_{0} y=b_{m} \frac{d^{m} u}{d t^{m}}+b_{m-1} \frac{d^{m-1} u}{d t^{m-1}}+\cdots+b_{1} \frac{d u}{d t}+b_{0} u $$ $[1.4]$ 여기서, $n \geq m$
1.2. Transfer Fucntion
전달함수transfer fuction은 입력과 출력의 관계를 주어주는 함수이며 아래와 같이 정의된다.
$$ G(s)=\frac{Y(s)}{U(s)} $$ $[1.5]$ 여기서, $Y(s)$, $U(s)$는 각각 $y(t)$, $u(t)$의 라플라스 변환
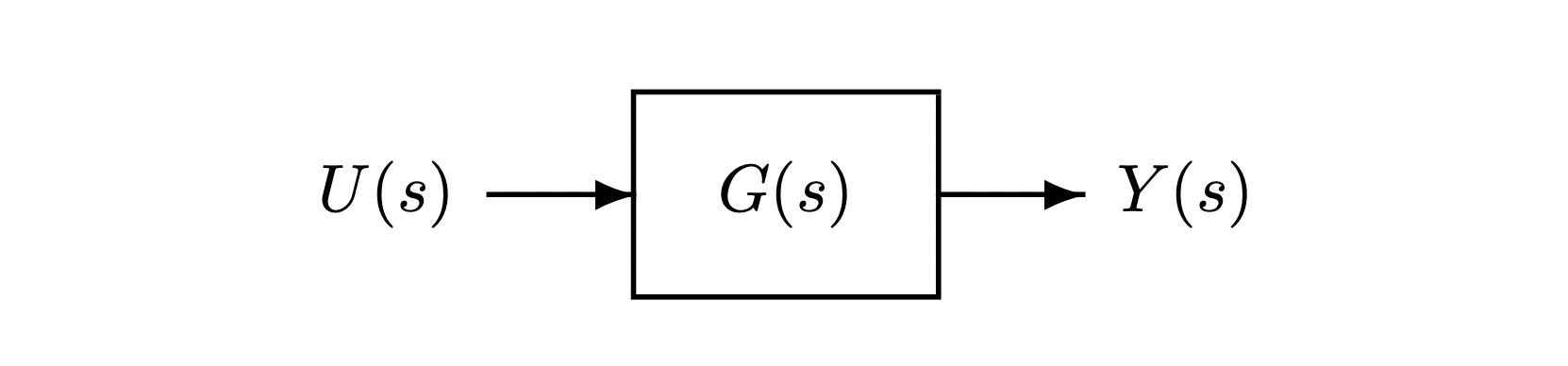
Laplace transform이다. 단, 모든 초기값은 $0$으로 둔다.$[Fig.\,1.2]$ Block diagram of System with Transfer Function $G(s)$
$[1.5]$식은 블록 다이어그램block diagram에 다라 $[Fig.\,1.2]$와 같이 나타내어진다. $s$는 미분연산 $d/dt$을 나타내는 기호 (연산자operator)라고 해석해도 된다.
예제 1.1. 다음 미분방정식으로 나타내진 시스템의 전달함수를 구해라.
\[\ddot{y}+a_{1} \dot{y}+a_{0} y=b_{1} \dot{u}+b_{0} u\][해답] 미분방정식을 모든 초기값이 $0$ ($y(0)=0, \dot{y}(0)=0, u(0)=0$) 이라는 조건하에 라플라스 변환을 하면
\[s^{2} Y(s)+a_{1} s Y(s)+a_{0} Y(s)=b_{1} s U(s)+b_{0} U(s)\]가 된다. 이제 전달함수로 다음 식을 얻는다.
\[\frac{Y(s)}{U(s)}=\frac{b_{1} s+b_{0}}{s^{2}+a_{1} s+a_{0}}\]위와 같이 미분방정식과 전달함수는 둘 다 수학 모델을 나타내고 있으며, 한 쪽에서 다른 쪽을 얻을 수 있다는 의미에서 등가(等価)이다. 다음으로 전달함수가 주어졌을 경우, 이에 대응하는 미분방적식을 구해보자.
예제 1.2. 다음 전달함수로 나타내진 시스템의 미분방정식 구해라.
\[\frac{Y(s)}{U(s)}=\frac{b_{1} s+b_{0}}{s^{2}+a_{1} s+a_{0}}\][해답] 전달함수 표현에서 다음 식을 얻는다.
\[s^{2} Y(s)+a_{1} s Y(s)+a_{0} Y(s)=b_{1} s U(s)+b_{0} U(s)\]이것을 시간영역 표현으로 바꾸면
\[\ddot{y}+a_{1} \dot{y}+a_{0} y=b_{1} \dot{u}+b_{0} u\]가 된다.
1.3. Default Transfer Function
간단한 시스템의 전달 함수나 시스템 구성 단위가 되는 전달 함수로서 다음의 기본 전달 함수가 있다. 비례 요소proportional element, 미분 요소derivative element, 적분 요소integral element, 1차 지연 요소(first-order lag element), 2차 요소(second-order element), 시간 낭비 요소(dead time element). 이들의 전달 함수를 $[Table\,1.1]$에 나타냈다.
예제 1.3. 비례요소의 시간영역 입출력 관계를 구해라.
[해답]
\[\frac{Y(s)}{U(s)}=K\]에서 시간영역 표현으로
\[y=K u\]를 얻을 수 있다.
| Element Name | $G(s)$ |
| Proportional Element | $K$ |
| Derivative Dlement | $s$ |
| Integral Element | $\frac{1}{s}$ |
| First-Order Lag Element | $\frac{1}{1+T s}$ |
| Second-Order Element | $\frac{\omega_{n}^{2}}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}}$ |
| Dead Time Element | $e^{-L s}$ |
$[Table\,1.1]$
예제 1.4. 1차 지연 요소의 시간영역 입력함수를 구해라.
[해답]
\[\frac{Y(s)}{U(s)}=\frac{1}{1+T s}\]여기에서
\[\frac{Y(s)}{U(s)}=\frac{1}{1+T s}\]시간영역으로 바꾸면
\[T \dot{y}+y=u\]이 된다.
예 1.1. (비례요소) 용수철 시스템: 힘을 $u$, 변위를 $y$, 용수철 상수를 $k$로 하면 다음 관계(훅의 법칙Hook's law)가 성립한다.
이것을 라플라스 변환을 하면
\[Y(s)=\frac{1}{k} U(s)\]가 된다. 여기서 전달함수로서 다음 식을 얻을 수 있다.
\[\frac{Y(s)}{U(s)}=\frac{1}{k}\]$[Fig.\,1.3]$ Spring System (Proportional Element) / $[Fig.\,1.4]$ RL Circuit System (Differential Element)
예 1.2. (미분요소) RL 회로 시스템: 전압 $v$와 전류 $i$와의 사이에 다음 관계가 있다.
\[v(t)=L \dot{i}(t)\]따라서, $I(s)$에서 $V(s)$까지의 전달함수는
\[\frac{V(s)}{I(s)}=L s\]가 된다.
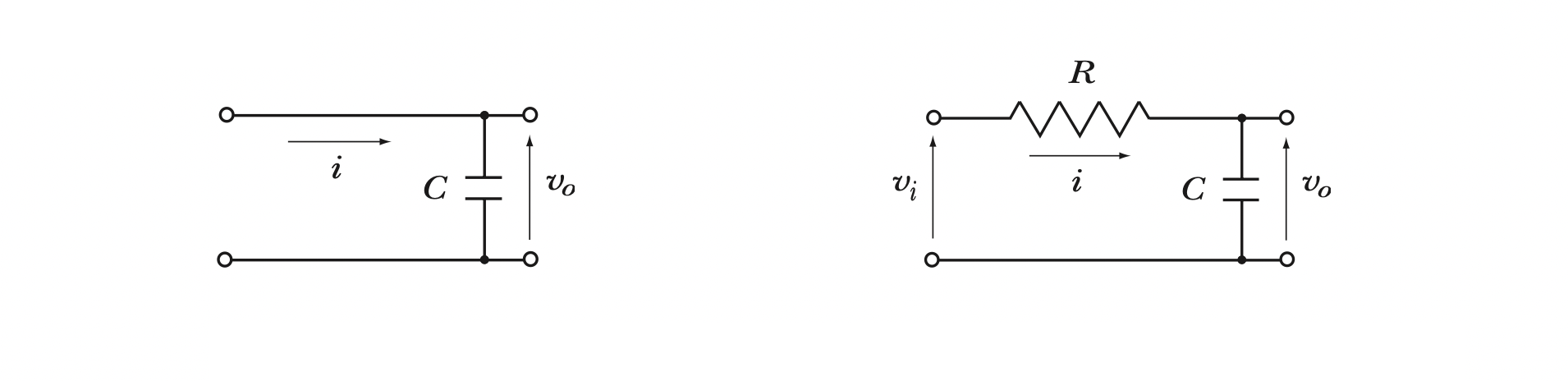
$[Fig.\,1.5]$ C Circuit System (Integral Element) / $[Fig.\,1.6]$ RC Circuit System (First-Order Lag Element)
예 1.3. (적분요소) C 회로 시스템: 전압 $v_o$과 전류 $i$와의 사이에 다음 관계가 성립한다.
\[v_{o}(t)=\frac{1}{C} \int i(t) d t\]이것을 $t$로 미분하면
\[\dot{v}_{o}=\frac{1}{C} i\]라플라스 변환하여
\[s V_{o}(s)=\frac{1}{C} I(s)\]따라서, $I$부터 $V_o$까지의 전달함수는
\[\frac{V_{o}(s)}{I(s)}=\frac{1}{C s}\]이 된다.
예 1.4. (1차 지연 요소) RC 회로 시스템: 전압의 평형식으로부터
\[R i(t)+v_{o}(t)=v_{i}(t)\]$v_o$과 $i$의 사이에는
\[v_{o}(t)=\frac{1}{C} \int i(t) d t\]즉
\[i(t)=C \dot{v}_{o}(t)\]라는 관계가 있으며, 이것을 이용해 정리하면
\[\dot{v}_{o}(t)=\frac{1}{R C}\left(v_{i}(t)-v_{o}(t)\right)\]를 얻을 수 있다. 또한, 라플라스 변환을 하면
\[s V_{o}(s)=\frac{1}{R C}\left(V_{i}(s)-V_{o}(s)\right)\]따라서, $V_i(s)$부터 $V_o(s)$까지의 전달함수는
\[\frac{V_{o}(s)}{V_{i}(s)}=\frac{1}{1+R C s}\]이 된다.
1.4. Exercise
다음 전달함수를 갖는 시스템의 시간영역 입출력 관계를 구해라.
(1) $\frac{Y(s)}{U(s)}=\frac{\omega_{n}^{2}}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}}$
(2) $\frac{Y(s)}{U(s)}=\frac{5(s+1)}{(s+2)(s+3)}$다음 미분방정식으로 표현되는 시스템의 전달함수를 구해라.
(1) $\dot{h}(t)=\frac{1}{C} q(t)$ 입력: $q$ 출력: $h$
(2) $L C \ddot e_{o}(t)+R C \dot e_{o}(t)+e_{o}(t)=e_{i}(t)$ 입력: $e_i$ 출력: $e_o$$[Fig.\,1.7]$의 2자유도계의 전달함수를 구해라. 단, $m_1$, $m_2$는 질량, $c_1$은 점성감쇠계수, $k_1$, $k_2$는 용수철 상수, $f$는 외력, $x_1$, $x_2$는 변위이다. 입력을 $f$, 출력을 $x_1$이라고 한다.
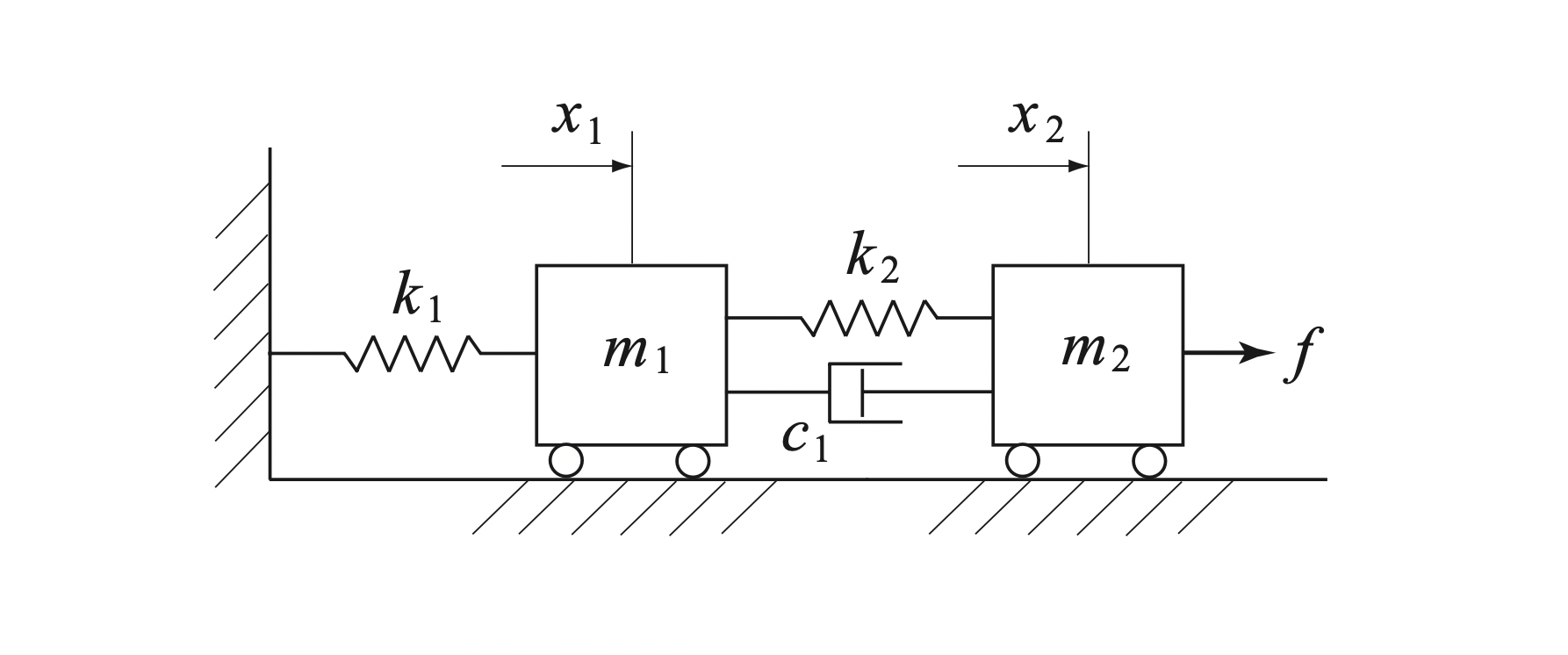
$[Fig.\,1.7]$ Damped Two-Degree System$[Fig.\,1.8]$의 직렬결합된 수조(水槽) 시스템의 전달함수를 구해라. 단, $q_1$은 기준유입량에서의 편차, $x_1$, $x_2$는 평형수위로부터의 편차, $C_1$, $C_2$는 수조의 단면적, $R_1$, $R_2$는 유출저항이다. 입력은 $q_1$, 출력은 $x_2$로 한다.
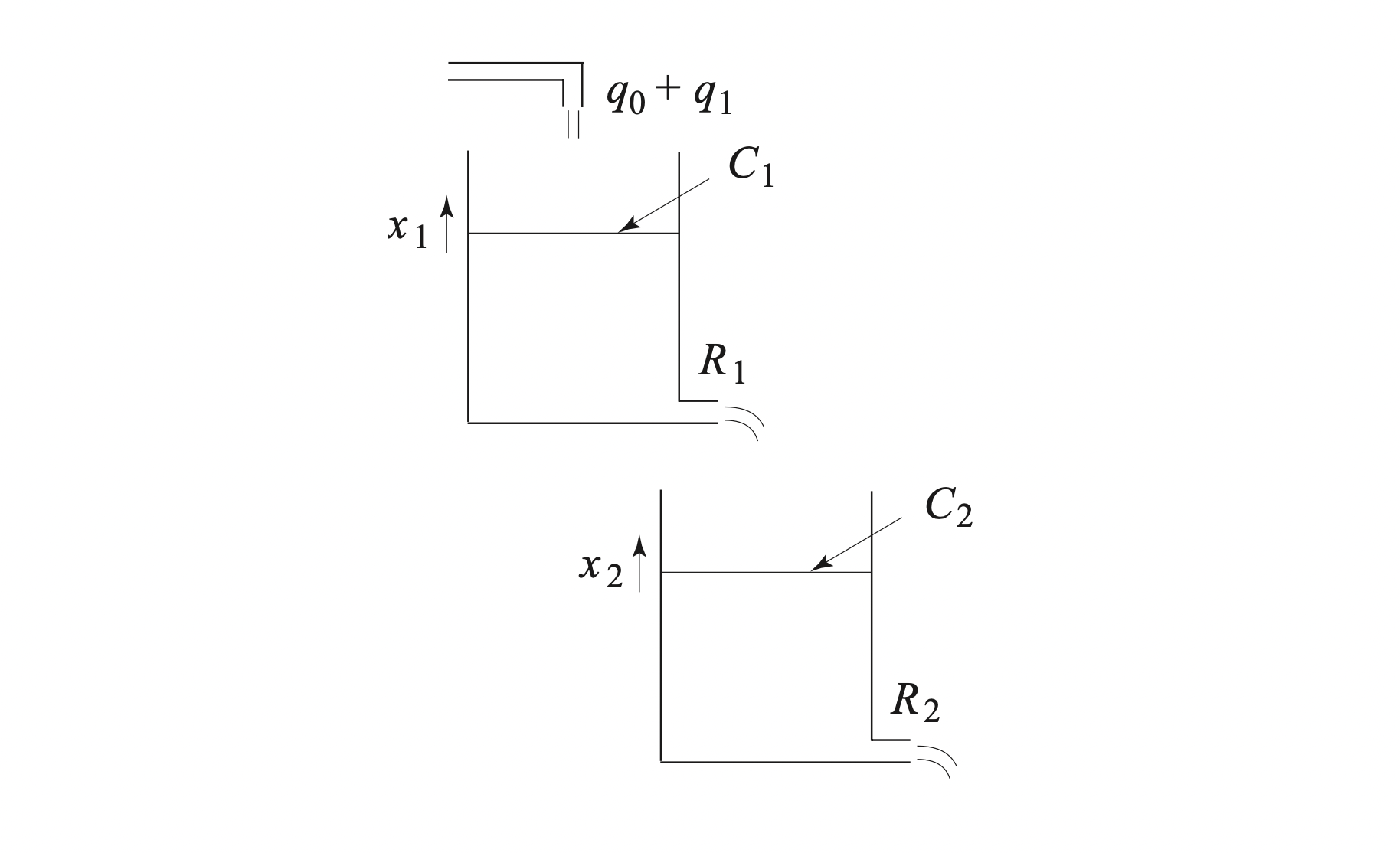
$[Fig.\,1.8]$ Aquarium System Coupled in Series$[Fig.\,1.9]$의 회로 시스템의 전달함수를 구해라. 입력을 $v_i$, 출력을 $v_o$로 한다.
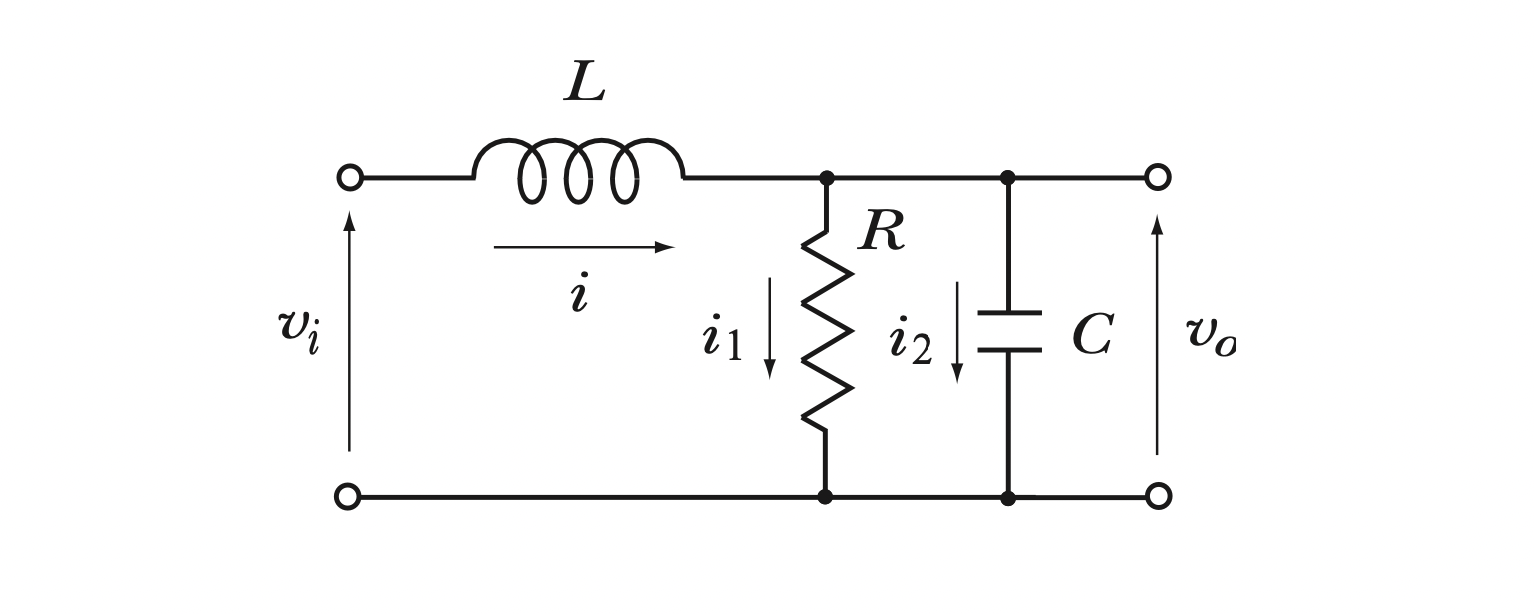
$[Fig.\,1.9]$ LRC Circuit System
[풀이]